Юриспруденция
- Адвокаты
- Административное право
- Возмещение вреда
- Воинский учет
- Гражданство
- ДТП, ОСАГО, ГИБДД
- Договорное право
- ЖКХ,ТСЖ,выселение
- Загранпаспорта, визы
- Интеллектуальная собств.
- Кредиты и займы
- Медицинское право
- Налоги
- Наследство
- Недвижимость
- ООО, АО, ИП
- Оценка имущества
- Потребительское право
- Правоведение
- Произвол чиновников
- Семейное право
- Социальное право
- Страховое право
- Судебные приставы
- Судебный эксперт
- Таможня
- Трудовое право
- Уголовное право
Все категории
- Медицина
- Акушерство и гинекология
- Аллергология (иммунология)
- Анестезиология
- Ветеринария
- Гастроэнтерология
- Гомеопатия
- Дерматология
- Диетология
- Инфектология
- Кардиология
- Наркология
- Неврология
- Нефрология
- Онкология
- Ортопедия
- Оториноларингология
- Офтальмология
- Педиатрия
- Психиатрия
- Ревматология
- Рентгенология
- Сексология
- Стоматология
- Терапия
- Травматология
- Урология
- Фармация
- Хирургия
- Эндокринология
- Красота, Здоровье
- Бизнес
- Дом, отдых, хобби
- Религия




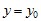 при
при